NAS MG
The NAS benchmark suite has been developed at NASA Ames Research Center as part of the Numerical Aerodynamic Simulation Program. It consists of 5 application kernels and 3 small application programs, which are considered representative for large scale applications in computational fluid- and aerodynamics. From this suite the application kernels MG and FT are chosen for evaluating SAC with respect to both ease and elegance of programming and runtime performance of compiled code.
Implementation
The NAS benchmark MG implements a V-cycle multigrid algorithm to approximate a solution u of the discrete Poisson equation $\nabla^2 u = v$ on a 3-dimensional grid with periodic boundary conditions. Rather than iteratively applying relaxation steps to a grid of fixed size as in the PDE1 benchmark, they are consecutively applied to grids of varying granularity, i.e., they are embedded within operations to coarsen and refine grids. The rationale for this approach is to accelerate the propagation of low-frequent defects across the original grid and, hence, to improve the convergence behaviour.
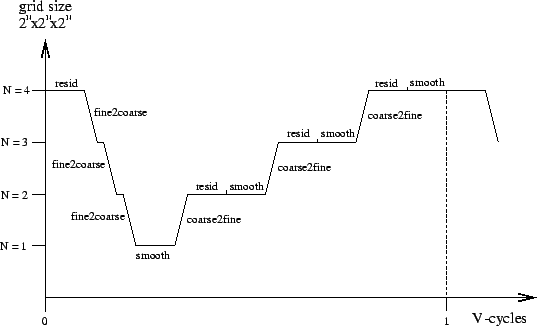
The Mgrid benchmark iteratively applies a V-cycle multigrid relaxation algorithm to a 3-dimensional grid. A single V-cycle consists of a recursive nesting of relaxation steps and smoothing steps on grids of varying granularity as well as of mappings between these grids. The figure and the SAC-code below illustrate a single V-cycle for a grid of $64^3$ elements. The order in which the different transformations are applied is depicted along the horizontal axis, whereas the grid size involved in each step is indicated along the vertical axis.
Following a top-down approach, this sequence of operations can easily be implemented by means of the two functions MGrid and VCycle shown in the SAC-code below. MGrid creates the initial solution grid u before it alternatingly computes the current residual and the correction of the current solution by means of a single V-cycle. The recursive function VCycle realizes exactly the sequence of basic operations, as is illustrated in the figure above. Both implementations almost literally coincide with their mathematical specifications.
double[+] MGrid( double[+] v, int iter) { u = genarray( shape(v), 0d); for( i=0; i<iter; i+=1) { r = v - Resid( u); u = u + VCycle( r); } return( u); } double[+] VCycle( double[+] r) { if (Coarsest( r)) { z = Smooth( r); } else { rn = Fine2Coarse( r); zn = VCycle( rn); z = Coarse2Fine( zn); r = r - Resid( z); z = z + Smooth( r); } return( z); }
Whereas arithmetic array operations used in the definitions of MGrid and VCycle are just imported from the SAC array library, additional implementations are required for relaxation and smoothing operations as well as for the mappings between grids of different size. A closer look at their specifications reveals that they uniformly contain single relaxation steps, which only vary with respect to weights associated with adjacent elements.
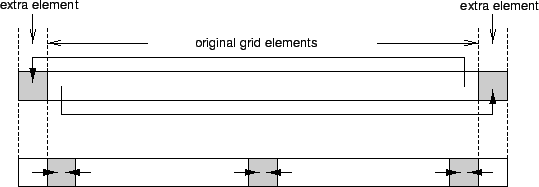
Implementing relaxation steps in SAC has already been addressed in PDE 1 Implementation. But whereas the PDE1 benchmark is characterized by fixed boundary conditions, NAS-MG uses periodic ones, i.e., the grid represents a torus rather than a cube. A solution which still allows for reuse of existing code is to artificially extend the original grid by additional boundary elements. More precisely, each original boundary element is replicated on the opposite side of the grid, as illustrated in the figure above. They allow to implement relaxation with periodic boundary conditions by two consecutive steps.
- Artificial boundary elements are initialized according to their location.
- An ordinary relaxation step is applied to the extended grid.
double[+] Resid( double[+] u) { u = SetupPeriodicBorder( u); u = RelaxKernel( u, A); return( u); } double[+] Smooth( double[+] r) { r = SetupPeriodicBorder( r); r = RelaxKernel( r, S); return( r); }
Based on the existing relaxation kernel as developed for the PDE1 benchmark, the four V-cycle operations can be implemented more or less straightforwardly. As shown in the code, implementations of Resid and Smooth boil down to setting up the periodic boundary elements followed by a single relaxation step. In fact, they only differ with respect to the weights associated with adjacent elements during the relaxation step. However, A and S are constant arrays defined by the benchmark specification.
double[+] Fine2Coarse( double[+] r) { rs = SetupPeriodicBorder( r); rr = RelaxKernel( r, P); rc = condense( 2, rr); rn = embed( shape(rc)+1, 0*shape(rc), rc); return( rn); } double[+] Coarse2Fine( double[+] rn) { rp = SetupPeriodicBorder( rn); rs = scatter(2, rp); rt = take( shape(rs)-2, rs); r = RelaxKernel( rt, Q); return( r); }
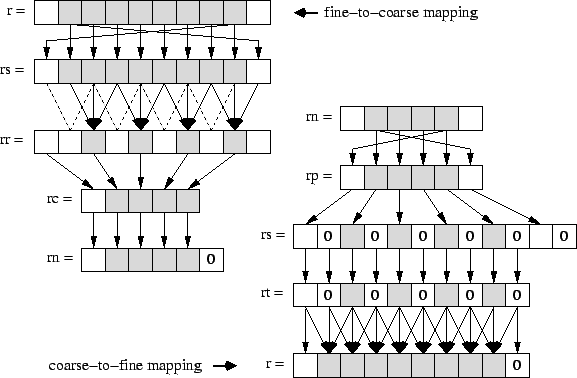
Implementations of the remaining V-cycle functions Fine2Coarse and Coarse2Fine are shown above. Besides applying additional relaxation steps similar to Resid and Smooth, but with yet different weights P and Q, they map fine grids to coarse grids and vice versa, as illustrated in the next figure. Both mapping steps can be realized by combinations of predefined array operations from the SAC library, whose implementations are shown in the code below.
The fine-to-coarse mapping is basically implemented by means of the function condense (str, a), which creates an array whose extent in each dimension is by a factor of str less than that of the given array a. Its elements are taken from applying a stride of str. However, due to the additional boundary elements, condense does not exactly match the fine-to-coarse mapping requirements, as the result array lacks one such element . Therefore, the intermediate array rc must subsequently be embedded into an array of correct size. This is specified by means of the library function embed( shp, pos, a), which creates a new array of shape shp, whose elements starting at index position pos are copied from the argument array a. Actually, the function embed is complementary to the function tile used for the specification of the relaxation kernel in PDE 1 Implementation.
The coarse-to-fine mapping is implemented by means of the library function scatter(str, a), which is complementary to condense. As illustrated , it creates an array which in each dimension is by a factor of str larger than the given array a. All elements of a are copied into every other location of the result array applying the given stride str; remaining elements are initialized by 0. However, due to the additional boundary elements, the resulting array is by two elements too large in each dimension; a subsequent application of the library function take removes them.
double[+] condense( int str, double[+] a) { ac = with (. <= iv <= .) genarray( shape(a) / str, a[str*iv]); return( ac); } double[+] scatter( int str, double[+] a) { as = with (. <= iv <= . step str) genarray( str * shape(a), a[iv/str]); return( as); } double[+] embed( int[.] shp, int[.] pos, double[+] a) { ae = with (pos <= iv < shape(a)+pos) genarray( shp, a[iv-pos]); return( ae); } double[+] take( int[.] shp, double[+] a) { at = with (. <= iv <= .) genarray( shp, a[iv]); return( at); }
Evaluation
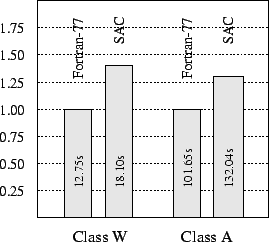
This section compares the runtime performance achieved by code compiled from the SAC specification of MG, as outlined in the previous section, with that of the FORTRAN-77 reference implementation coming with the NAS benchmark suite NAS Source. The settings of the following experiments are exactly the same as described in PDE1 Evaluation. Similar to the PDE1 benchmark, timing is restricted to multigrid iterations and, thus, ignores startup and finalization overhead. Several size classes are defined by the benchmark rules, two of which are selected for the following experiments:
- Class W: initial grid size 64 x 64 x 64 and 40 iterations,
- Class A: initial grid size 256 x 256 x 256 and 4 iterations.
The figure shows the single processor runtime performance achieved by SAC and by FORTRAN-77 for both size classes. In fact, the FORTRAN-77 program outperforms the compiled SAC code by 29.6% and by 23.0% for size classes W and A, respectively. Despite its considerably higher level of abstraction, the SAC specification achieves runtime performance characteristics which are in the same range as the rather well-tuned low-level FORTRAN-77 reference implementation. Moreover, performance differences diminish with increasing problem size.
A closer look at the FORTRAN implementation reveals that to a large extent a tricky hand optimizations of the stencil operation is mainly responsible for its superiour runtime performance. Symmetry properties in the definitions of the 4 different stencils used in relaxation operations are exploited not only within single iterations, but computations are also shared across iterations. Whereas a 27-point stencil, as used in the benchmark, in general, incurs 27 multiplications and 26 additions per iteration, the number of multiplications may be reduced to only 4 by taking into account that actually just 4 different weights occur in the stencil definition. This is realized by both FORTRAN and SAC. However, the FORTRAN code additionally stores results of computations shared among different iterations due to such symmetries in auxiliary buffers and, thus, reduces the number of additions to values between 12 and 20 depending on the concrete stencil.
This explains why in previous performance evaluations on this benchmark, SAC has been reported to outperform FORTRAN-77 by about 10%. Whereas preceding investigations were based on version 1.0 of the NAS benchmark suite, the experiments described here involve the most recent version 2.3, which comes with significantly improved reference implementations.
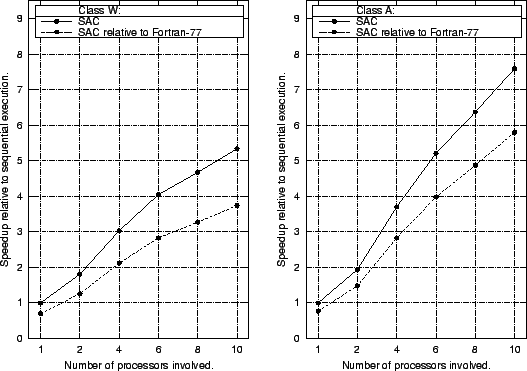
The figure above shows the runtime performance of SAC code implicitly compiled for multithreaded execution. Relative to sequential execution, speedups of up to 4.8 and up to 7.6 are achieved for size classes W and A, respectively. In fact, size class A is the smallest one intended for benchmarking, whereas size class W is specifically designed for program development on uniprocessor PCs and workstations.
The main scalability limitation arises from the repeated reduction of the grid size during the V-cycle. Whereas multithreaded execution pays for relatively large grids on the top end of the V-cycle, runtime overhead increasingly reduces its benefit for smaller grids on the bottom. Below a threshold grid size, all operations are actually performed sequentially to avoid excessive overhead. This sequential kernel of the NAS-MG benchmark limits its scalability, but its actual impact on performance decreases with growing initial grid size. Therefore, considerably higher speedups are achieved for size class A than for size class W.
Although, this problem is algorithm-inherent rather than implementation-specific, its impact on runtime performance is actually increased by dynamic memory management, as employed by SAC. Since the absolute overhead incurred by it is invariant against grid sizes involved, it is negligible for large grids but shows a growing performance impact with decreasing grid size. As a consequence, the sequential kernel of NAS-MG, where operations are performed on very small grids, is considerably more expensive with dynamic memory management in SAC than it is with a static memory layout in a low-level FORTRAN-77 implementation.
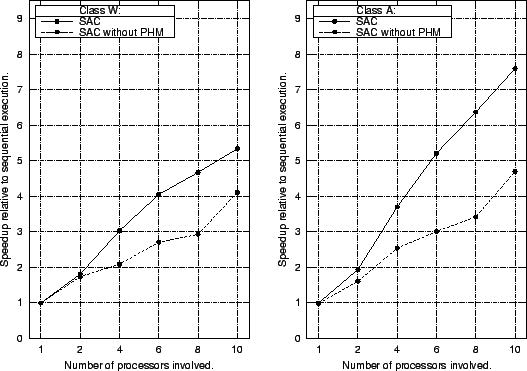
To investigate the effect of the SAC-specific memory manager, on the runtime performance of this benchmark, the experiment is repeated with private heap management disabled. Its outcome is shown above. Whereas single processor performance is hardly affected by the choice of the memory allocator, it has a significant impact on scalability. Maximal speedups relative to sequential execution drop from 4.82 to 3.55 for class W and from 7.63 to only 4.63 for class A.
However, the performance degradation may not be attributed to scalability limitations in the design of the SOLARIS standard allocator. In fact, all memory allocations and de-allocations in compiled code are performed in single-threaded execution mode. It is merely their general performance, which increases the time spent in sequential operations on small grids at the bottom of the V-cycle.