Table of Contents
PDE1
The PDE1 benchmark approximates solutions to 3-dimensional discrete Poisson equations by means of red/black successive over-relaxation. It has previously been studied in compiler performance comparisons in the context of HPF, and reference implementations are available with HPF compilers. Implementation sketches out the PDE1 benchmark and its HPF implementation, before some alternative SAC implementations are discussed. Their runtime performance is compared to that of the HPF code in Evaluation.
Implementation
The kernel of the PDE1 benchmark is a stencil operation, which is iteratively applied to a 3-dimensional grid for a given number of times. The stencil operation itself is rather trivial: for each inner grid element at some index position $(i,j,k)$, the values of the 6 directly adjacent elements are summed up, are added to a fixed number $h^2f_{i,j,k}$ and are subsequently multiplied by a constant factor. However, in the case of red/black relaxation, this stencil operation is not applied to all inner grid elements in a single step, but is restricted to two disjoint subsets in two consecutive steps. These sets are called the red set and the black set. For the PDE1 benchmark, the red set consists of those elements with an even index in the outermost dimension whereas the black set refers to the remaining elements with an odd index.
DO NREL=1,ITER ! ! RELAXATION OF THE RED POINTS ! WHERE(RED(2:NX-1,2:NY-1,2:NZ-1)) U1(2:NX-1,2:NY-1,2:NZ-1) = & & FACTOR*(HSQ*F(2:NX-1,2:NY-1,2:NZ-1)+ & & U(1:NX-2,2:NY-1,2:NZ-1)+U(3:NX,2:NY-1,2:NZ-1)+ & & U(2:NX-1,1:NY-2,2:NZ-1)+U(2:NX-1,3:NY,2:NZ-1)+ & & U(2:NX-1,2:NY-1,1:NZ-2)+U(2:NX-1,2:NY-1,3:NZ)) END WHERE WHERE(RED(2:NX-1,2:NY-1,2:NZ-1)) U (2:NX-1,2:NY-1,2:NZ-1) = U1 (2:NX-1,2:NY-1,2:NZ-1) END WHERE ! ! RELAXATION OF THE BLACK POINTS ! WHERE(.not. RED(2:NX-1,2:NY-1,2:NZ-1)) U1(2:NX-1,2:NY-1,2:NZ-1) = & & FACTOR*(HSQ*F(2:NX-1,2:NY-1,2:NZ-1)+ & & U(1:NX-2,2:NY-1,2:NZ-1)+U(3:NX,2:NY-1,2:NZ-1)+ & & U(2:NX-1,1:NY-2,2:NZ-1)+U(2:NX-1,3:NY,2:NZ-1)+ & & U(2:NX-1,2:NY-1,1:NZ-2)+U(2:NX-1,2:NY-1,3:NZ)) END WHERE WHERE(.not. RED(2:NX-1,2:NY-1,2:NZ-1)) U (2:NX-1,2:NY-1,2:NZ-1) = U1 (2:NX-1,2:NY-1,2:NZ-1) END WHERE ENDDO
The source code shows the relevant part of the HPF reference implementation, where NX, NY, and NZ denote the extents of the grid in the three dimensions and U represents the grid itself. The relaxation step is specified by aggregate array operations using the HPF triple notation. The restriction of the stencil operation to either the red set or the black set of elements is realized by embedding it within a where-construct. An additional 3-dimensional constant array of booleans called RED serves as a mask for the selection of either red or black elements. However, two where-constructs are needed for specifying each of the two relaxation steps. In fact, re-computed grid elements are temporarily stored in an auxiliary array U1 and, hence, must be copied back to U after each relaxation operation.
This HPF implementation of PDE1 can be carried over to SAC more or less straightforwardly. The stencil operation may be implemented in SAC by means of a single WITH-loop, as illustrated by the definition of the function Relax. It is specified from the perspective of a single grid element at some index position iv and then mapped to all inner grid elements by means of the WITH-loop generator.
double[.,.,.] Relax( double factor, double hsq, double[.,.,.] f, double[.,.,.] u) { u1 = with (. < iv < .) { sum = u[iv+[1,0,0]] + u[iv-[1,0,0]] + u[iv+[0,1,0]] + u[iv-[0,1,0]] + u[iv+[0,0,1]] + u[iv-[0,0,1]]; val = factor * (hsq * f[iv] + sum); } modarray (u, iv, val); return( u1); }
However, this implementation of the relaxation step has a drawback just as the HPF code: it is tailor-made for the given stencil and for the given problem dimensionality. Although stencil operations are fairly common, these restrictions make opportunities for reusing the given implementation in contexts other than the PDE1 benchmark rather unlikely. With the explicit specification of constant offset vectors this SAC implementation does not significantly exceed the level of abstraction achieved by using the triple notation in HPF.
double[+] Relax2( double factor, double hsq, double[+] f, double[+] u, double[+] weights) { u1 = with (. < iv < .) { blk = tile( shape(weights), iv-1, u); sum = sum( weights * blk); val = factor * (hsq * f[iv] + sum); } modarray( u, iv, val); return( u1); }
To raise the level of abstraction, and thus to improve opportunities for code reuse, it is desirable to abstract as far as possible from the problem specific part of the relaxation operation, in particular from dimensionality and from stencil layout. This can be achieved by providing the function Relax with an additional parameter which yields an abstract specification of the stencil by means of an array of weights. This alternative implementation is shown above. For the specific needs of the PDE1 benchmark, weights is an array of shape [3,3,3] with all elements being set to 0 except for the six elements directly adjacent to the central element, which are set to 1. In SAC, this can be specified as
weights = reshape( [3,3,3], [ 0d,0d,0d, 0d,1d,0d, 0d,0d,0d, 0d,1d,0d, 1d,0d,1d, 0d,1d,0d, 0d,0d,0d, 0d,1d,0d, 0d,0d,0d ]);
As shown the function Relax2, extracts a subarray blk from the argument array u, whose shape is identical to that of the given array of weights. This is done by means of the library function tile( shp, offset, array), which creates an array of shape shp, whose elements are taken from array starting at index position offset. The computation of the weighted sum of adjacent elements thus turns into sum( weights * block), where ( array * array ) refers to an element-wise multiplication of arrays, and sum( array) sums up all elements of array. As outlined in the next example, these library functions can all be implemented by a single WITH-loop each.
double[+] tile( int[.] shp, int[.] offset, double[+] array) { blk = with (. <= iv <= .) genarray( shp, array[pos+iv]); return( blk); } double sum( double[+] array) { s = with (0*shape(array) <= iv < shape(array)) fold( +, 0d, array[iv]); return( s); } double[+] * (double[+] a, double[+] b) { m = with (. <= iv <= .) genarray( min( shape(a), shape(b)), a[iv] * b[iv]); return( m); }
Abstracting from a concrete stencil actually has two benefits. On the one hand, the resulting specification supports different stencil layouts without altering the definition of Relax2. On the other hand, the function Relax2 may be applied to arrays of any dimensionality, again without modifying its implementation. This is reflected by changing the respective type declarations from double[.,.,.] to double[+] (see Representation of Arrays for a discussion of SAC array types).
Nevertheless, the specification of Relax2 still is specific to the PDE1 benchmark as it explicitly implements the arithmetic operations involving factor, hsq, and f on an element-wise basis. However, to improve opportunities for code reuse, it is desirable to clearly separate application specific code from more generally applicable code. This is achieved by the definition of the function RelaxPDE1, as shown below. Whereas RelaxPDE1 itself contains the benchmark specific part of the relaxation step, the more general relaxation kernel of summing up some adjacent array elements based on an array of weights is isolated within a separate function definition.
double[+] RelaxPDE1( double factor, double hsq, double[+] f, double[+] u, double[+] weights) { rel = factor * (hsq * f + RelaxKernel( u, weights)); rel = CombineInnerOuter( rel, u); return( rel); } double[+] RelaxKernel( double[+] u, double[+] weights) { rel = with (. < iv < .) { blk = tile( shape(weights), iv-1, u); sum = sum( weights * blk); } modarray( u, iv, sum); return( rel); } double[+] CombineInnerOuter( double[+] inner, double[+] outer) { res = with (. < iv < .) modarray( outer, iv, inner[iv]); return( res); }
Rather than being specified element-wise as in preceding implementations of the PDE1 relaxation step, the arithmetic operations involving factor, hsq, and f are realized by means of the respective aggregate array operations, which are provided by the SAC array library. However, they effect all elements of the involved arrays in a uniform way rather than being limited to the inner ones, as is required by PDE1 to keep boundary elements unchanged. Therefore, the additional function CombineInnerOuter is employed for their subsequent correction. As shown above, this function takes two identically shaped arrays inner and outer as arguments and creates a new array whose inner elements are taken from inner whereas its boundary elements are taken from outer. Similar to the implementation of RelaxKernel, the function CombineInnerOuter is completely unspecific to the PDE1 benchmark and may be reused in any suitable context.
With an appropriate implementation of the PDE1 relaxation step at hand we may now focus on its extension to red/black relaxation. Actually, the effect of relaxation is to be restricted to two disjoint subsets of grid elements, i.e. to the red set and to the black set, as discussed in the beginning of this section. In analogy to the HPF implementation they are represented by a single boolean array red, which is initialized according to the specifications of the PDE1 benchmark. Whereas in HPF the restriction of the stencil operation to either the red or to the black elements is specified by means of the built-in where-construct, exactly the same functionality may be provided in SAC by means of a function where, as defined below. Being a generalization of the previously defined function CombineInnerOuter, it takes as arguments a boolean array mask and two arrays a and b. Assuming that all three arguments are of equal shapes, it creates a new array whose elements are taken either from a or from b, depending on the respective value of mask.
double[+] where( bool[+] mask, double[+] a, double[+] b) { c = with (. <= iv <= .) genarray( shape(mask), mask[iv] ? a[iv] : b[iv]); return( c); } double[+] RedBlack( double factor, double hsq, double[+] f, double[+] u, double[+] weights, bool[+] red, int iter) { for (nrel=1; nrel<=iter; nrel+=1) { u = where( red, RelaxPDE1( factor, hsq, f, u, weights), u); u = where( !red, RelaxPDE1( factor, hsq, f, u, weights), u); } return( u); }
Based on this implementation of where, red/black successive over-relaxation may be specified as shown. Note that the resulting function RedBlack, which basically implements the PDE1 benchmark, is invariant against the problem dimensionality as well as against variations of the stencil layout. In its definition, the black set is referred to by !red, i.e., by using the element-wise extension of the negation operator, as defined in the SAC array library.
Evaluation
This section compares the runtime performance of the SAC implementation of the PDE1 benchmark with that of the HPF reference implementation. The machine used in the following experiments is a 12-processor SUN Ultra Enterprise 4000 shared memory multiprocessor, running SOLARIS-7. The SUN Workshop compiler cc v5.0 is used as back end compiler for SAC. The HPF implementation is compiled by the ADAPTOR v7.0 HPF compiler developed at GMD (German National Research Center for Information Technology). The SUN Workshop compiler f77 v5.0 is used to transform the resulting FORTRAN-77 intermediate code into host machine code. Non-sequential execution of HPF programs is based on the shared memory version of PVM 3.4.2 as low-level communication layer.
The HPF implementation of PDE1 is directly taken from the benchmark suite coming with ADAPTOR. It employs cubic grids whose sizes are powers of two; use of timers excludes startup overhead inflicted by the initialization of data structures and of the underlying communication layer from benchmark results. In the absence of timing facilities in SAC, all experiments are repeated with two different numbers of iterations, and differences in program execution times are taken as benchmark results. This allows for comparing SAC and HPF on a reasonably fair basis.
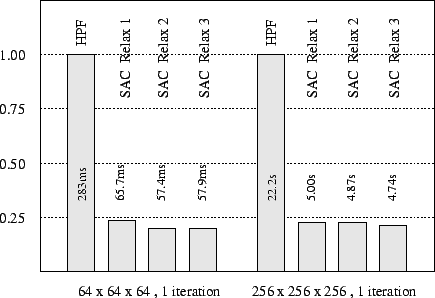
The next image shows single processor benchmark results for two problem sizes: 643 and 2563 Average times needed to complete a single red/black relaxation step are given for the HPF reference implementation as well as for the SAC implementation discussed in the previous section. All three alternative specifications of the core relaxation operation are investigated. However, regardless of which one is taken, the SAC implementation outperforms its HPF counterpart by factors of between 4 and 5 for both problem sizes.
Despite considerably varying levels of abstraction characterizing the different implementations of the relaxation kernel, their runtime performance is nearly the same. Surprisingly, the first, least abstract specification is even outperformed by the others by up to 10%. Whereas the SAC compiler by means of thorough optimization manages to compile all three different specifications to almost identical intermediate representations, a rather subtle variation is responsible for this observation. The element-wise specification leads to compiled code which extracts all 6 stencil elements from the argument array before it performs any arithmetic operations on them. In contrast, the more abstract specifications shown in both result in compiled code which executes memory load instructions alternatingly with arithmetic computations and, thus, to some extent, hides memory latencies by overlapping them with productive computations.
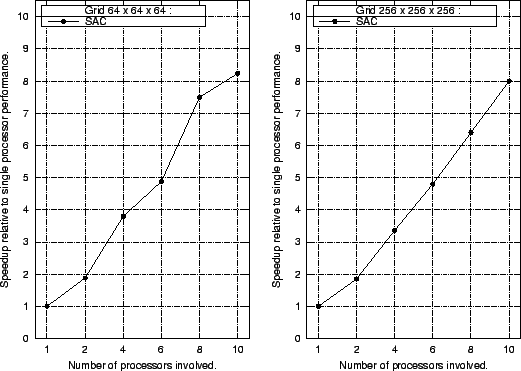
The next plots show speedups achieved by compiling the SAC implementation of PDE1 for implicit multithreaded execution. Due to the very similar sequential performance characteristics of the different SAC specifications, all investigations with respect to multithreaded execution are limited to the final, most abstract variant. In fact, the compiled SAC code for both problem sizes scales well with increasing numbers of processors engaged. Speedups of more than 8 are achieved with 10 processors. Simultaneously engaging more than 10 out of 12 processors is hardly profitable because the machine used for the experiments is not operated in batch mode and, hence, other system and user processes are constantly present.
Whereas performance improvements scale smoothly for the larger grid, it can be observed that certain processor counts are better suited for the smaller grid than others, e.g. 2, 4, and 8. However, this may easily be attributed to the scheduling scheme which achieves a better balanced workload distribution if the number of processors exactly divides the grid size in the outermost dimension. This effect is increasingly noticeable for grids which are small relative to processor counts.
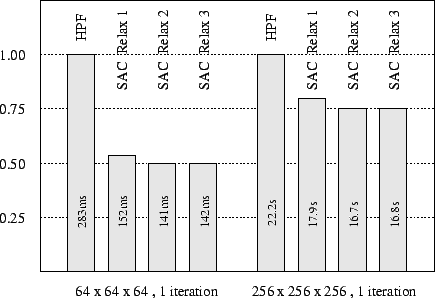
Experiences made with a similar stencil operation show that the investigated problem sizes are particularly sensitive against cache utilization. To quantify the effect of cache optimizations on the runtime performance of the SAC implementation, the experiment is repeated with cache optimizations disabled. In fact, only array padding and array placement need to be disabled as the tile size inference heuristic decides not to apply tiling to both problem sizes under consideration. The next figure shows the outcome of this experiment. As expected, cache optimizations, in particular array padding, turn out to be crucial for the runtime performance of compiled SAC code. Nevertheless, even with all cache optimizations disabled, SAC still outperforms HPF.
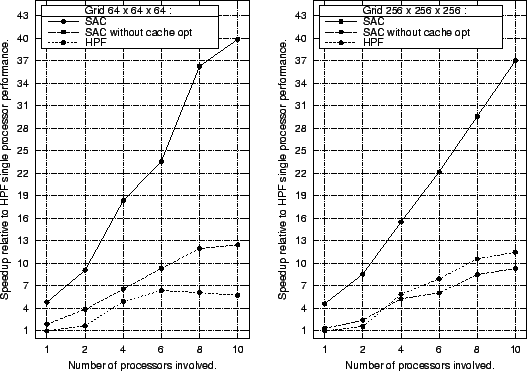
The next figure shows the multiprocessor performance achieved by both SAC and HPF, given as speedups relative to HPF single processor performance. Once again, it shows the significance of cache optimizations for the runtime performance of compiled SAC code. Without them SAC is outperformed by HPF for the larger grid size $256^3$ when using more than 4 processors.
In fact, super-linear speedups are achieved by the HPF code. This can be attributed to the fact that being based on message passing HPF employs a different memory data layout for each number of processors used. These changes implicitly eliminate cache conflicts, which to some extent are responsible for the relatively poor sequential performance of HPF. In contrast, the multithreaded execution model of SAC reuses the memory data layout used in sequential execution without modification and, thus, may not benefit from similar effects.
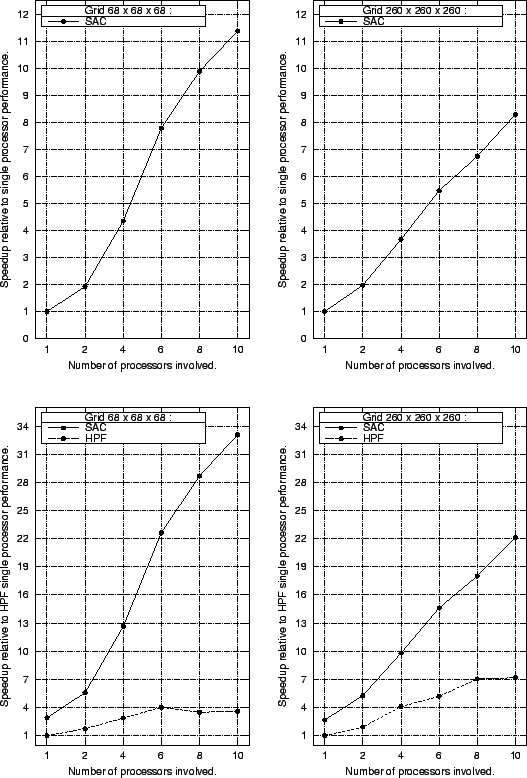
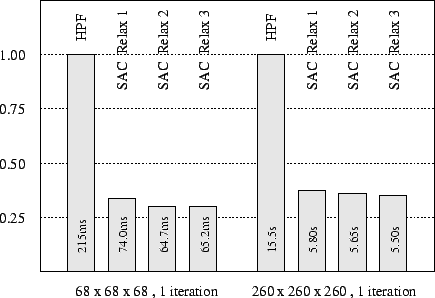
For both problem sizes investigated, it turns out that cache conflicts actually dominate runtime performance. Their elimination either by respective optimization techniques as in SAC or, more or less accidentally, through data layout transformations as in HPF is the crucial issue. To mitigate such effects, the experiment is once again repeated with slightly different problem sizes, which are less likely to incur systematic cache conflicts. The next figure shows the respective single processor benchmark results for grid sizes of $68^3$ and $260^3$ elements. It turns out that in the absence of significant numbers of cache conflicts SAC still outperforms HPF by factors of about 3. Comparing these results with those of the last figure shows that without cache optimizations SAC suffers much more from cache conflicts in the original problem sizes than HPF does. This may indicate that either the HPF compiler or the FORTRAN-77 back end compiler apply some cache optimizations as well.
 |
| Multiprocessor runtime performance of SAC and HPF |
 |
| Single processor performance for alternative grid sizes |
Last but not least, the plot below shows the multiprocessor runtime performance achieved for the two alternative problem sizes. Speedups are given both for SAC relative to its single processor performance as well as for SAC and HPF relative the HPF single processor performance. Whereas for the grid size $260^3$ SAC achieves similar speedups as for the grid size $256^3$, super-linear speedups can be realized for the grid size $68^3$ when using 4 processors or more. This behaviour may be attributed to the fact that 4 processor specific L2 caches of 1MB each are sufficient to cover the entire memory requirements inflicted by this grid size. By careful memory data layout the number of main memory accesses may thus be considerably reduced compared with execution by a single processor. However, at the time being, it is not quite clear why no similar speedups are achieved for grids of size $64^3$, despite careful cache optimization.
Without accidentally reduced cache conflicts, speedups achieved by HPF are considerably lower for the alternative grid sizes than for the original ones.