Table of Contents
Implementation
Support for Complex Numbers
SAC does not provide a built-in data type for the representation of complex numbers. However, they can easily be mimicked by vectors of two floating point numbers. The typedef construct allows to abstract from this implementation by introducing a user-defined type complex. With this type definition at hand, the usual arithmetic and relational operators can be overloaded with implementations on complex numbers. Embedding the type definition and a basic set of operations within a SAC module provides all what is needed for processing complex numbers on a high level of abstraction.
The following code sketches out such a module implementation:
ModuleImp Complex: typedef double[2] complex; complex toc(double[2] d) { return((:complex) d); } double[2] tod(complex c) { return((:double[2]) c); } double real(complex c) { return( tod(c)[[0]]); } double imag(complex c) { return( tod(c)[[1]]); } complex + (complex a, complex b) { return( toc( [real(a)+real(b), imag(a)+imag(b)])); } complex * (complex a, complex b) { real = real(a)*real(b) - imag(a)*imag(b); imag = real(a)*imag(b) + imag(a)*real(b); return( toc( [real, imag])); } complex == (complex a, complex b) { return( (real(a)==real(b)) && (imag(a)==imag(b))); }
Following the type definition of complex, the two functions toc and tod provide basic facilities for converting 2-element double vectors into complex numbers and vice versa. Their implementations are based on special cast expressions in SAC, which allow for conversion between defined types and their underlying definitions. The two conversion functions encapsulate this functionality in a more convenient way. Note that this implementation of tod overloads the built-in operation for converting integers or single precision floating point numbers into a representation of type double.
Various customized conversion operations may be implemented by means of the basic ones. With them at hand, basic arithmetic and relational operations on complex numbers can be implemented rather straightforwardly, as illustrated above. Overloading of the usual infix operators allows for handling complex numbers just as other numerical data. However, the NAS-FT benchmark also requires processing of arrays of complex numbers. Hence, usual element-wise extensions of scalar operations, reduction operations, and structural array operations need to be provided as well.
Implementation Aspects
The NAS benchmark FT essentially implements 3-dimensional complex fast-Fourier transforms. Although the benchmark rules are unspecific with respect to concrete algorithms, both the FORTRAN-77 reference implementation as well as the SAC specification discussed in the following implement 3-dimensional FFTs by consecutive collections of 1-dimensional FFTs, as illustrated in the picture. An array of shape [X,Y,Z] is consecutively interpreted as a ZY field of vectors of length X, as a ZX field of vectors of length Y, and as a XY field of vectors of length Z. On each of these vectors, a 1-dimensional FFT is performed.
The outline of this algorithm can be carried over into a SAC specification more or less straightforwardly, as shown in the code below. The function FFT3d consecutively transposes the argument array a three times. After each transposition, 1-dimensional FFTs are performed on vectors extracted along the innermost dimension by means of the function SliceFFT. The transposition vectors used in applications of the library function transpose are chosen to consecutively transform the original array into arrays of shapes [Z,Y,X], [Z,X,Y], and back to [X,Y,Z]. The additional parameter rofu provides a pre-computed vector of complex roots of unity, which is used for 1-dimensional FFTs.
complex[.,.,.] FFT3d( complex[.,.,.] a, complex[.] rofu) { a_t = transpose( ([2,1,0]), a); b = SliceFFT( a_t, rofu); b_t = transpose( ([0,2,1]), b); c = SliceFFT( b_t, rofu); c_t = transpose( ([1,2,0]), c); d = SliceFFT( c_t, rofu); return( d); } complex[.,.,.] SliceFFT( complex[.,.,.] a, complex[.] rofu) { res = with( [0,0] <= iv < [shape(a)[[0]],shape(a)[[1]]] ) { slice = FFT( a[iv], rofu); } modarray( a, iv, slice); return( res); }
By means of a single WITH-loop, SliceFFT extracts all subvectors along the innermost dimension of the complex argument array. Note in the application of FFT, the overloading of the sel function for the selection of complex subarrays, which also allows for reusing its special notation. A regular 1-dimensional complex FFT is then performed on each of the vectors by an application of the function FFT, whose implementation is shown in the next source code.
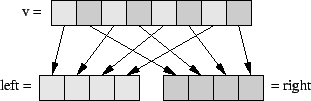
complex[.] FFT(complex[.] v, complex[.] rofu) { if (shape(v)[[0]] > 2) { left = condense(2, v); right = condense(2, rotate( [-1], v)); rofu_select = condense(2, rofu); fft_left = FFT( left, rofu_select); fft_right = FFT( right, rofu_select); fft_right = fft_right * rofu; res = cat( fft_left + fft_right, fft_left - fft_right); } else { res = [v[[0]]+v[[1]] , v[[0]]-v[[1]]]; } return( res); }
The function FFT almost literally implements the Danielson-Lanczos algorithm , which is based on the recursive decomposition of the argument vector v, as illustrated in below. Two vectors, named left and right, take its elements from even and from odd index positions, respectively. The vector left can simply be created by an application of the library function condense. The function condense has already been used in the implementation of the NAS benchmark MG and, thus, is a good example for code reuse made possible through the high=level APL-like programming style pursued by SAC. In fact, it may be reused once again for creating the vector right by rotating the argument vector by one index position to the left beforehand. This can easily be accomplished by an application of the library function rotate.
The fast-Fourier transform is then recursively applied to both vectors, left and right. Subsequently, one of the two transformed vectors, i.e. fft_right, is multiplied with the respective elements of the pre-computed vector of complex roots of unity. Note that * here refers to the element-wise complex product. In each incarnation of FFT, the length of the vector rofu is half that of v. Hence, fft_right and rofu are of the same length and, thus, can be multiplied without additional measures. However, for each recursive application of FFT, those elements of rofu must be selected which are needed in the following recursion step. This is specified by means of another application of condense. Finally, element-wise, complex sum and difference of the two recursively Fourier transformed vectors are computed, and the results are concatenated by means of the library function cat. Once the length of the argument vector reaches 2, a direct implementation of the fast-Fourier transform on a 2-element complex vector terminates the recursion.